Laplace transform
Given a complex-valued function $f(t)$ with $t\in \mathbb{R}$, the Laplace transform is a function $F:\mathbb{C}\to \mathbb{C}$ such that every $F(s)$ represents the weight of the function $e^{st}$ in the decomposition
$$ f(t)=\frac{1}{2\pi i}\left( \cdots+F(c+0.1i)e^{(c+0.1i)t}+F(c+0.2i)e^{(c+0.2i)t}+\right. $$ $$ \left.+F(s)e^{st}+\cdots\right)= $$ $$ =\frac{1}{2 \pi i} \lim _{T \rightarrow \infty} \int_{c-i T}^{c+i T} e^{s t} F(s) d s $$for any $c\in \mathbb{R}$
In this video it is pictured like this:
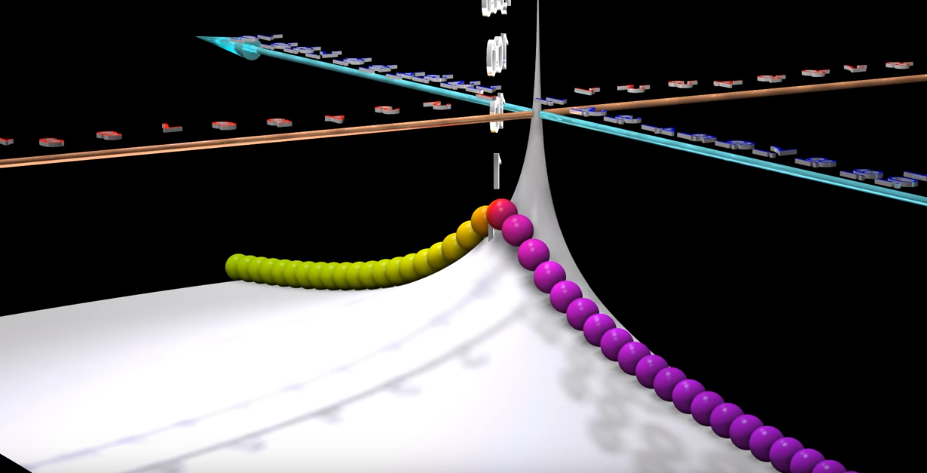
A particular case would be the Fourier transform, whose picture corresponds to the case $c=0$
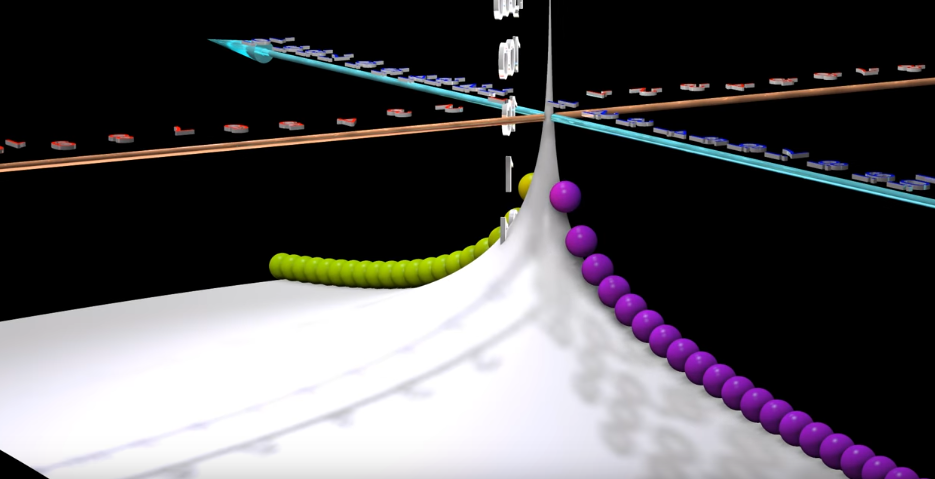
Both transformations has to do with the fact that some spaces of functions are Hilbert spaces, so we have a "basis". The original function can be thought as expressed in the Dirac delta basis, and the Fourier transform and Laplace transform are nothing but the expression of the same function in a different basis.
What basis?, the natural for the generator of the translation and momentum operators.
Related: Mellin transform.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: